ENG | How image downsampling works

I wanted to find out how difficult is to implement magic kernel sharp downsampling filter from John Costella, because I like it’s output which is basically without aliasing and it’s sharp at the same time. I’ll leave out theory behind the filter - it’s better to read original page or PDFs. Code itself is public domain (MIT-0 license) and it’s used by Facebook and Instagram.

It turns out that image processing is done in the following steps:

1. Apply sRGB->linear RGB mapping (basically gamma correction)
2. Downsample image using magic kernel filter

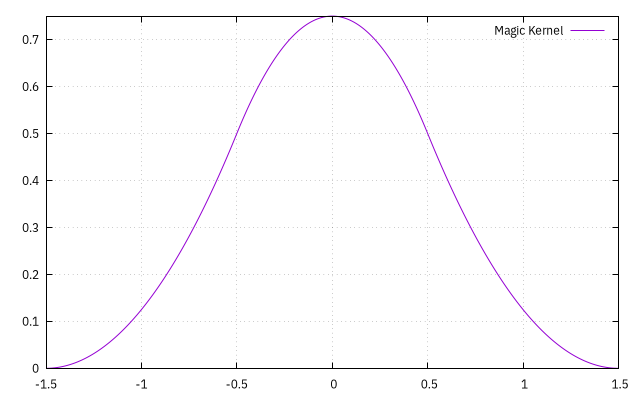
   static inline double magic_kernel(double x)
   {
       if (x < 0.0)
           x = -x;
       if (x <= 0.5)
           return(0.75 - (x * x));
       if (x < 1.5)
           return(0.5 * (x - 1.5) * (x - 1.5));
       return 0.0;
   }
   

   

3. Optional, highly recommended: apply sharpening 3x3 kernel (magic kernel sharp 2013) {-0.25*s, 1+0.5*s, -0.25*s}, where s=1 for facebook (MKS), s=1.32 for instagram (MKS+)
   or apply different kernel without oversharpening {−1, +6, −35, +204, −35, +6, −1} / 144
4. Apply linear RGB -> sRGB conversion (undo gamma correction)

Steps 2 and 3 can be combined together which is done in some image processing libraries that do not allow multiple passes.

Steps 1. and 5. were already explained in article about color spaces:

Pro-Tip: Whenever when you are dealing with image processing or rendering, at least consider doing gamma correction before and after image operations like resampling, blurring. I know this for roughly 15 years and it was a surprise, considering I’ve dealt with all of this professionally. Some tools like GIMP, ImageMagick, Paint.NET handle it correctly. FastStone Image Viewer does not. Effect is not always obvious, correction using two pow function is not cheap, but here is an example

Image blur with and without gamma correction.

Step 3. is obvious to me.

However step 2. is not. I always assumed that image downsampling is implemented as low pass filter (such as gaussian blur) with sigma roughly the same as downsampling factor and kernel size roughly three sigma and next step is regular sampling (or bilinear one). I was actually quite close. These two steps can be merged and we can compute only pixels used in the output image. At the same time we can evaluate kernel weights based on distance from output pixel instead of doing bilinear filtering.

If resampling filter is separable (can be applied by rows, then by columns rather then square - most simple filters have this property), we can just precompute kernels for each row and column of image.

So downsampling works like this (simplified to grayscale, pseudocode)

* determine downsampling factor/scale e.g. src_width=5120, dst_width=512, scale=10
* determine support radius in source image `radius = support_width * scale`. Magic kernel has support_width=1.5 so radius=15
* for each row ...
*   for dx = 0..dst_columns                  // for each destination pixel
*     float src_x: ((dx+0.5) * scale) - 0.5  // for dx=0: (0+0.5)*10-0.5=4.5, for dx=511: (511+.5)*10=5114.5
*     int_x  = (int)src_x                    // e.g 4
*     frac_x = src_x - int_x                 // e.g 4.5-4=0.5
*     sum_w = sum = 0
*     for (int kx=[-radius..radius], step=1) // from -15 to 15 included, kernel_width=31
*       int sx = wrap_index(ix+kx, src_cols) // wrap source x (sx) at zero or src_cols, for example 11,10,9...1,0,1...17,18,19 - centered at 4 going from -11 to 19
*       float dx_dist = fabs(frac_x-kx)/scale  // get kernel distance at pixel (e.g 1.55, 1.45, 1.35 ... 0.05, 0.05 ... 1.35, 1.45)
*       if (dx_dist>support) continue;       // out of range -> 0
*       double w = KernelFunc(dx_dist)       // evaluate kernel weight
*       sum   += w * src_row[sx]             // weighted sum of pixels
*       sum_w += w                           // total weight
*     dst_row[dx] = sum / sum_w              // normalize (edge case if sum_w=0 skipped for simplicity)

A bit confusing part is that image has coordinates 0..511, width 512 and centers of first and last pixel are 0.5 and 511.5.

And similar code works for rows. Filter is separable. We are applying 31x1 and 1x31 filters instead of 31x31 which is much more expensive, especially since we are evaluating kernel per pixel, rather precomputing it for every destination column.

NOTES

• Original article claims that in order to implement downsampling on hardware, image can be upsampled and then bilinear sampling can be used
• It also states that for upsampling, sharpening is applied first.